Surviving zombie apocalypse with random search algorithm
Introduction
Imagine a typical Hollywood zombie apocalypse scenario…
A group of desperate folks, led by a charismatic hero, barricades itself in some building, trying to make it to the end of the movie. Hoards of blood craving creatures knock on every door and every window trying to get inside. The people try to back them off using anything they can, but as they are getting short on ammo, the hero needs to send somebody to fetch more shells.
The decision has to be made - weighing the risks of losing a team member against running out of ammo. Doesn’t it sound like an optimization problem?
Although it certainly can be formulated this way, we will see that it is not always possible to apply the standard gradient descent algorithm (SGD). Instead, we will use a simple alternative known as the random search. To illustrate its simplicity, we will implement it in pure python .
Our survival scenario
Let’s assume, for the sake of argument, that our charismatic hero has a laptop with a text editor (e.g. vim if he’s a real hero) and python3 installed - just enough to quickly run a simulation and find out what to do.
The situation presents itself as follows:
- There are N days of peril, during which they have to make it.
- As soon as the (N + 1)-th day comes, the military will come to rescue the survivors.
- Until then, the team consumes one chest of ammo a day, and complete depletion equals inevitable death.
- Furthermore, the ammo loses its anti-zombie quality with every passing day, making it unusable after E days.
- The group starts with X chests of ammo.
- On designated days D = {d_1, d_2, …, d_K}, the airforce drops additional pods with chests of ammo to support the struggling men, and these days are known upfront.
- Unfortunately, there is a risk associated with recovering a chest from a pod. It is expressed as p in [0, 1] and represents the probability of losing a group member.
- Furthermore, with every chest taken from a pod, the risk increases quadratically with the number of chests retrieved.
- Finally, there is no need to accumulate any ammunition beyond the “zero-day”, as the military will promptly take it all away.
- Now, the challenge is to ensure that the team never runs out of ammo, while trying to minimize potential human sacrifice.
Building a model
The situation looks rather complex, so our first step is to build a model. We will use it to simulate different scenarios, which will help us to find the answer. This step is somewhat equivalent to the forward pass in SGD.
We know that the system is completely described using N, E, X and pairs of (d_k, p_k). Therefore, it is convenient to implement our model as a class and expose the method run to perform our forward pass.
Let’s start with a constructor.
1
2
3
4
5
6
7
8
E = 30 # expiry of anti-zombie serum
X = 10 # initial ammo supply
class Survival:
def __init__(self, total_days, pods, supplies_init=[E]*X):
self.total_days = total_days
self.pods = pods
self.supplies = supplies_init
The pods is a list of tuples representing the incoming ammo pods with associated risk of retrieval (e.g. [(10, 0.1), (20, 0.2)]). Since the supplies run out, we represent it as list of “days-to-expire”. Once the list gets empty - it’s over!
Next, to account for shrinking supplies, we define the following protected method:
1
2
3
4
def _consume(self):
self.supplies.remove(min(self.supplies))
self.supplies = list(map(lambda x: x - 1, self.supplies))
self.supplies = list(filter(lambda x: x != 0, self.supplies))
Every day one chest of ammo is consumed (line #3), then all supplies get one day closer to expiry (#4) and finally, the expired ones get removed from the list (#5).
Another thing happens when new supplies are retrieved.
1
2
3
4
def _retrieve(self, risk, quantity):
new_ammo = [E] * quantity
cost = quantity**2 * risk
return new_ammo, cost
In every case when we generate more ammo, we also increase the fractional risk that is proportional to how many chests we choose to retrieve from the pod. (If the cost > 1, we can treat is as the probability of losing more than one man).
To facilitate the forward pass, let’s define one more function:
1
2
3
4
5
def _get_risk(self, day):
pod = list(filter(lambda x: x[0] == day, self.pods))
if len(pod) > 0:
return pod[0][1]
return None
The function simply picks the risk associated with a pod that is scheduled for a given day (if it is scheduled).
Finally, the essence of the forward pass:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
def run(self, retrieval_plan):
total_risk = 0
retrieval_idx = 0
for day in range(1, self.total_days + 1):
risk_involved = self._get_risk(day)
if risk_involved:
new_ammo, partial_risk = self._retrieve(
risk_involved,
retrieval_plan[retrieval_idx])
self.supplies += new_ammo
total_risk += partial_risk
retrieval_idx += 1
if len(self.supplies) == 0:
return 0, total_risk, day
else:
self._consume()
return len(self.supplies), total_risk, day
The procedure starts with some retrieval_plan (more on that later) and the total risk is zero. Then, as we move day by day, there will be “opportunities” to acquire ammo. In case such opportunity exists on a particular day, we try to retrieve some particular amount of ammo given our retrieval plan. Whenever there are risk points involved, we add them to the overall risk count.
Then, regardless if we got more ammo or not, we check the status of our supplies. If we reached the end, this night will be the team’s last. The function returns 0 ammo left, the total sacrifice and the day to commemorate. If not, the team consumes the ammo while heroically defending their stronghold and the function returns the corresponding values.
This is all we need from our forward pass. Now, let’s look at the optimization.
Solution
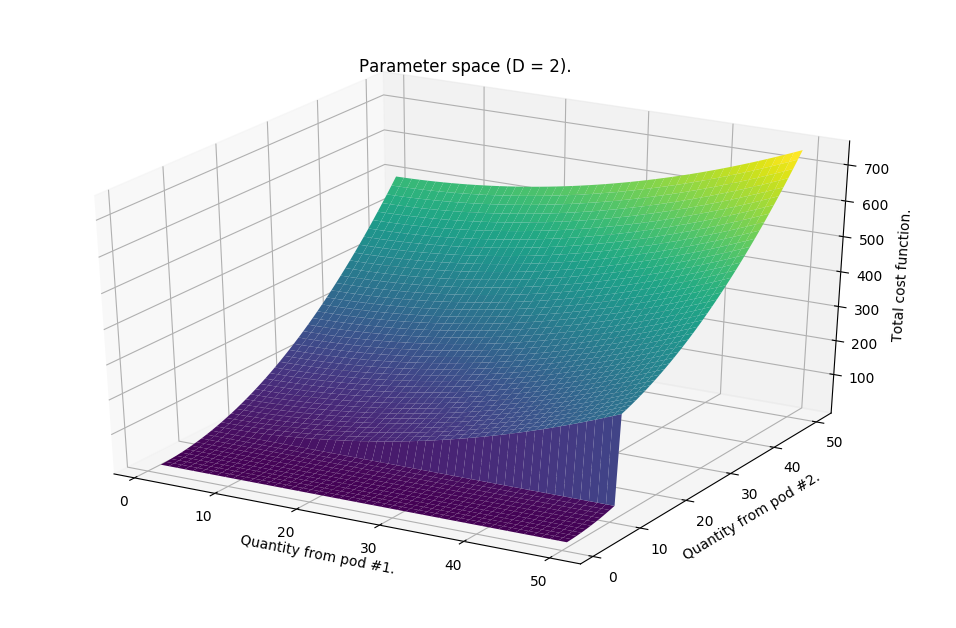
Under typical circumstances that would involve the standard gradient descent, we would now be designing the back-propagation pass and discussing how to properly implement the gradient. However, here there is no gradient! The function that describes the risk accumulation is more of a procedure. It is not differentiable. (No zombies are involved either…)
Because of that, and because of the number of constraints that we mentioned earlier, we need to think of another way to lower the risk. This is how the random search algorithm comes in.
The basic principle goes a follows:
- We define a cost function that is a way of measuring how “bad” the solution is. (In our example it is the total risk or losing team members).
- We initialize the system at random in the search space (z).
- We sample a new position (z’) in our search space from within the neighborhood of (z).
- We evaluate the cost and if lower, we move to that point (z’ -> z).
We repeat 3. and 4. as many times as it takes to improve and we can apply a hard stop if, for example, the cost no longer decreases, the time runs up, etc.
Of course, this approach does not guarantee that we find the best possible solution, but neither the SGD does that. Intuitively, however, we can think that we should find a possibly better solution if we continue to question the “status quo” and make small improvements.
Let’s take a look at the implementation. First, the initalization:
1
2
3
4
def initialize_retrieval_plan(pods, total_days):
a = list(map(lambda x: x[0], pods))
a.append(total_days)
return [a[x + 1] - a[x] for x in range(len(a) - 1)]
The function accepts the schedule of pods (list of {d_k, p_k}) and the number of days to survive, and returns a possible plan that describes how much ammo the team could retrieve at each opportunity - it is a list of integers.
Perhaps you have noticed there are no random numbers involved. Exactly - we do not initialize it randomly. Random initializations work well in case there is no preference of where to start. As our zombie-crisis is full of constraints, we can begin from the position of where at least one of the constraint can easily be satisfied. Therefore, we start with a plan that will guarantee the survival, giving the folks just enough bullets to make it.
From then on, we can optimize.
1
2
3
4
5
6
def calculate_plan(total_days, pods,
epochs=300,
supplies=[E]*X,
attempts=12,
radius=4):
...
The function calculate_plan is our alternative to the back-propagation step. We can think of epochs, attempts and radius as hyper-parameters, where epochs is a number search steps, attempts is a number of the points we sample under each step and radius expresses the “stretch” of the neighborhood of (z).
Because of the calculations can, in principle, take some time, the first thing that we do is to check if the conditions aren’t ill-suited or if the plan proposed won’t make them die. For example, if the date of the first pod comes after the team runs out of supplies, there will be no chance to resupply and the death is inevitable. In this case, we can just as well stop calculating and start praying.
1
2
3
4
5
6
7
8
plan = initialize_retrieval_plan(pods, total_days)
if is_illegal(plan):
print("This retrieval plan cannot make them survive.")
return
S = Survival(total_days, pods, supplies.copy())
supplies_size, cost, day = S.run(plan)
if day < total_days:
return
The is_illegal function is a simple check if no elements of the plan is negative (def is_illegal(plan): return (True in [c < 0 for c in plan])).
Having checked the feasibility, we can finally start optimizing for the minimal risk. The dimensionality of our parameter space equals the number of pods (that equals the length of plan). Sampling of that space means to pick an element of plan at random and see what happens if we remove some number of chests from a pod. However, to prevent violating the condition that the team must not run out of the ammo, we also pick another element of plan to give this quantity to. That creates a new plan that we verify using S.run(plan) to obtain a new outcome.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
plan_range = range(len(plan))
cost_history = [9999999] # initializing cost history for early stopping
last_plan = plan.copy()
epoch = 1
while epoch < epochs:
cache = {}
for attempt in range(attepmts):
i1 = random.choice(plan_range)
i2 = random.choice(plan_range)
plan = last_plan.copy()
qty = random.choice(range(1, radius + 1))
plan[i1] -= qty
plan[i2] += qty
S = Survival(total_days, pods, supplies.copy())
supplies_size, cost, day = S.run(plan)
The series of the if-else statements then checks for the remaining constraints, but if the new plan is feasible, we add it to cache that contains all alternative plans for the step with an associated cost function. Then, if there exists an alternative for which the cost function is lower, we choose that plan for the next iteration (z’ -> z).
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
if supplies_size < 0: # ran out of ammo
continue
elif day < total_days: # ran out of days
continue
elif is_illegal(plan): # attempt to sell ammo
continue
else: # solution found
key = '-'.join([str(x) for x in plan])
cache[key] = cost
last_plan, cost = get_minimum(cache)
print (f"{epoch}, cost: {cost}, plan: {last_plan}")
epoch += 1
cost_history.append(cost)
if cost_history[epoch - 1] == cost_history[epoch - 2]:
break
At some point there will be no further plan for a given step. When that happens, we fall back on the last feasible plan to be the solution.
1
2
3
4
5
6
if len(cache) == 0:
print ("No solution for this case. They must die.")
return
else:
print (f"Solution found, but it'll cost = {cost}.")
return last_plan
The get_minumum function is our custom version of arg min:
1
2
3
4
def get_minimum(cache):
min_risk = min(cache.values())
key = list(cache.keys())[list(cache.values()).index(min_risk)]
return [int(x) for x in key.split('-')], min_risk
Potential problems and alternatives This is it! Running, for example:
1
2
3
4
5
6
if __name__ == '__main__':
pods = [(10, 0.2), (15, 0.1), (35, 0.5), (50, 0.3)]
total_days = 70
plan = calculate_plan(total_days, pods)
print(plan)
we can see the progression in finding better plans and the cost value going down.
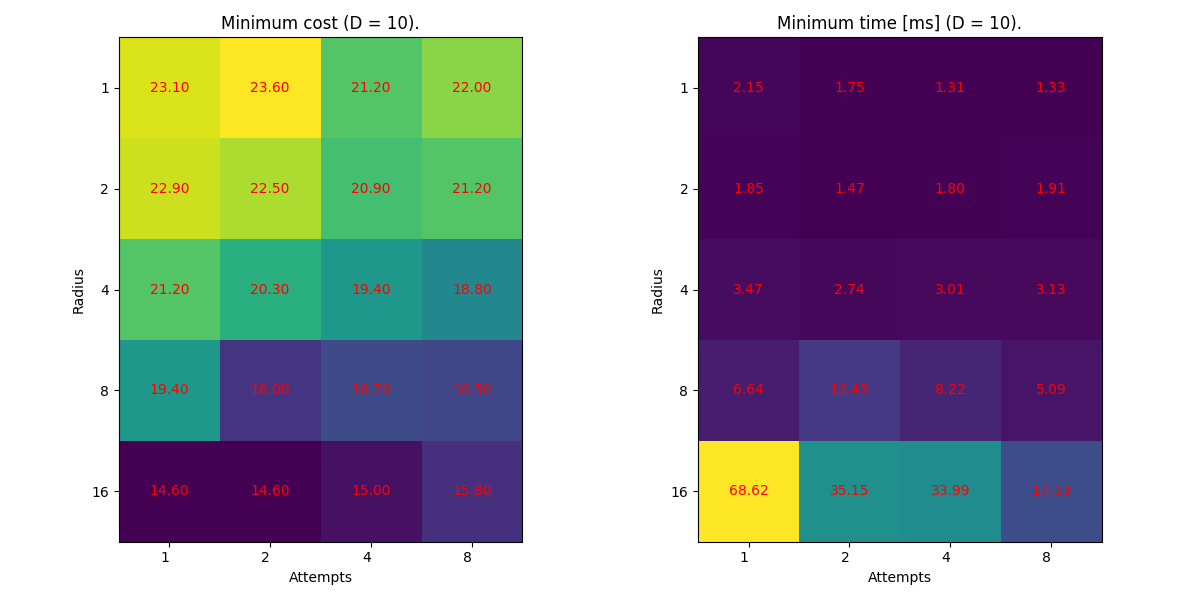
Unfortunately, if we execute this optimization a couple of times, we will quickly spot that the most “optimal” plan varies, and the cost value is higher at times than the others. This is because our algorithm is “blind”. Without gradient, we only give it a couple of shots (attempts) at every iteration to look for a better plan and we do so at random. Consequently, there is a significant threat that the algorithm gets to a place (z`) it can no longer progress - something like the local minimum.
To overcome this issue, we can naturally increase the number of attempts to give it more chance or radius to allow for more alternatives in finding better z’.
In an extreme case, we can choose to loop over all pairs of (z, z’) of a distance radius. This approach would be equivalent to brute-forcing the gradient, drastically increasing our chance of reaching the global minimum. On the other hand, there is a price to pay. With only radius == 1, the number of combinations (z, z’) is proportional to K ** 2, where K = len(plan). The computations can take longer.
Conclusions
Defending against hoards of the undead is, indeed, a major challenge. Zombies apart, in this article, we have presented an easy, bare-python implementation of the random search algorithm. This algorithm can be a feasible alternative to the SGD whenever we can define a cost function, but we cannot ensure its differentiability. Furthermore, if the problem is filled with constraints, like this one, the approach presented here can be applied. Finally, we have also discussed the computational complexity of the algorithm itself, which may impact the next hero’s decision if there is indeed a major zombie crisis.
